
Aplikasi ini menghitung perkiraan waktu tunggu menggunakan hukum Little dalam teori antrian.
Terima kasih telah memilih aplikasi ini!
[Aplikasi]
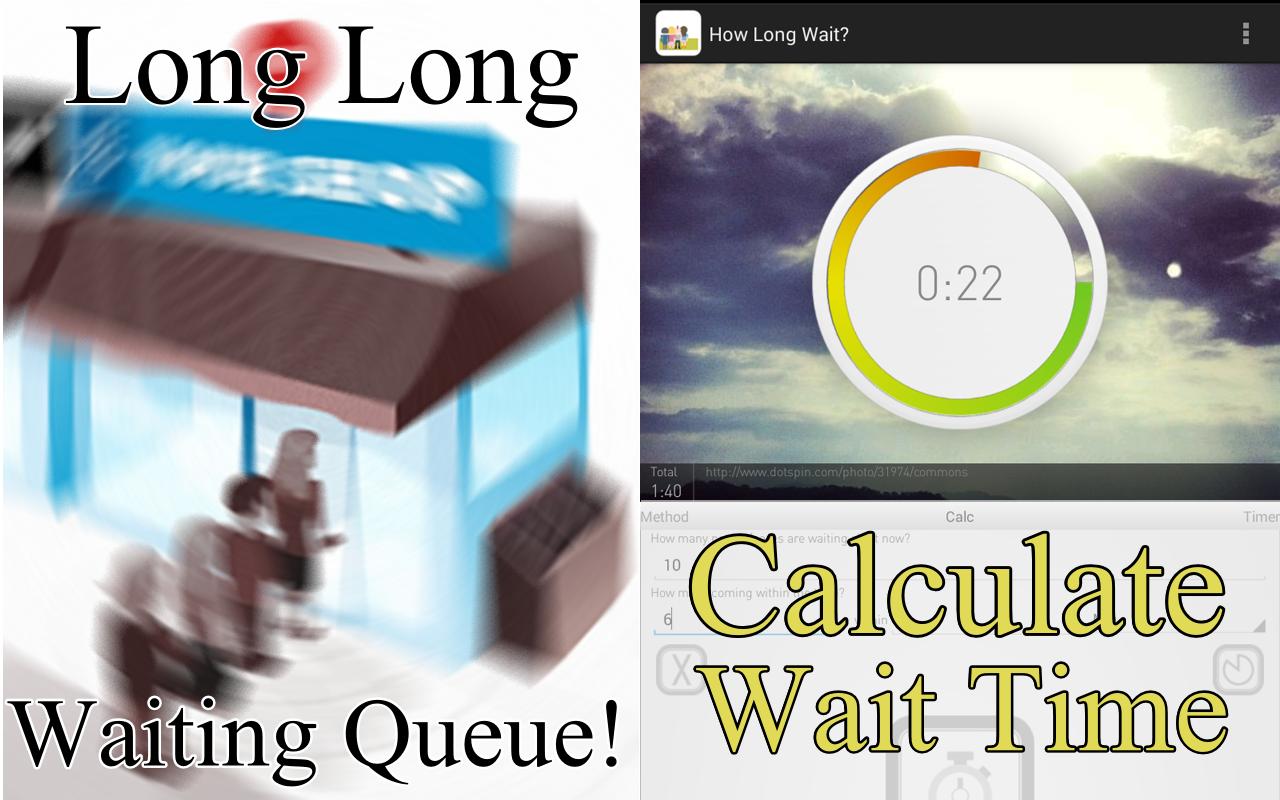
Terkadang kita harus menunggu dalam antrian ...
Pernahkah Anda berpikir akan menyenangkan jika saya bisa memperkirakan berapa lama saya harus menunggu?
Aplikasi ini menghitung perkiraan waktu tunggu menggunakan hukum Little dalam teori antrian.
Persyaratannya adalah panjang antrian tidak berubah seiring waktu dan non-preemptive.
Semoga aplikasi ini sedikit menyembuhkan ketidakpuasan Anda :-)
[Fitur]
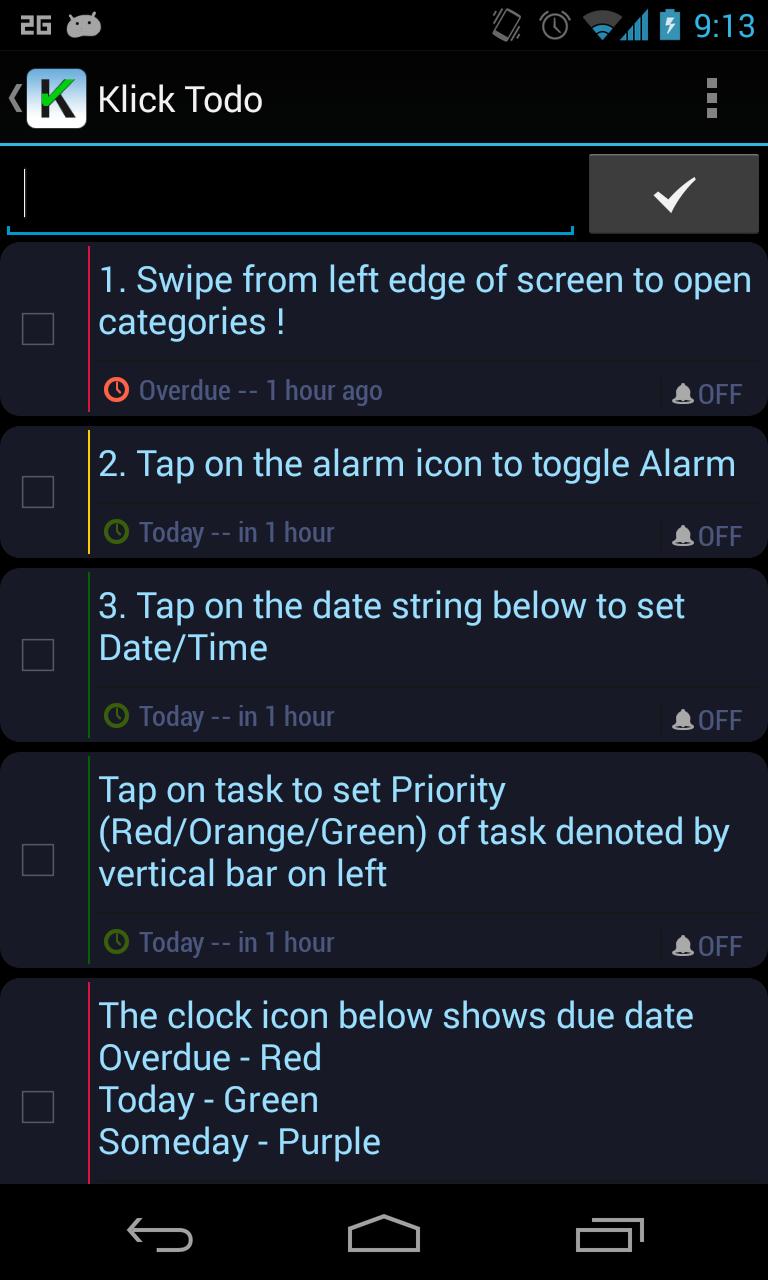
Mudah dan intuitif untuk digunakan, tombol besar dan menggesek
Tampilan kemajuan yang dapat dipahami untuk waktu tunggu dengan gradasi
Fungsi pengatur waktu untuk menghitung jumlah orang/pasangan dalam waktu
Beberapa pilihan format waktu kemajuan
Perbarui wallpaper selama waktu tunggu dengan animasi
Pemberitahuan saat waktu tunggu selesai.
Bagikan perkiraan waktu tunggu dengan teman -teman Anda!
Dukungan Tablet, Potret dan Lansekap
Tidak ada iklan (untuk versi berbayar)
Offline tersedia (untuk versi berbayar)
[Hukum Little]
L = jumlah orang/pasangan
λ = tingkat kedatangan orang/pasangan
W = Perkirakan Waktu Tunggu
Formula Hukum Little adalah
L = λ x w
λ juga disebut tingkat kedatangan efektif.
Ini menunjukkan berapa banyak orang/pasangan akan datang per satuan waktu
Dan semakin tinggi nilainya, semakin banyak orang/pasangan akan datang.
Dalam distribusi Poisson, setara dengan tingkat rata -rata.
Hukum atau formula adalah teorema oleh Profesor John Little (MIT) pada tahun 1961.
Hukum cukup universal karena tidak dipengaruhi oleh distribusi proses kedatangan,
Distribusi Layanan, Pesanan Layanan.
[Contoh Hukum Little 1]
- 10 orang sedang menunggu di toko
- 4 orang tiba dalam 1 menit
Oleh Hukum Little 、
L = 10
λ = 4
W = l / λ = 10/4 = 2.5
Jawaban: 2 menit 30 detik untuk menunggu
[Contoh Hukum Little 2]
- 8 orang menunggu di meja tunai
- 2 orang tiba dalam 10 detik
Oleh Hukum Little 、
L = 8
λ = 2
W = L / λ = 8/2 (10 detik waktu satuan)
Jawaban: 40 detik untuk menunggu